Números Complexos
Daniel Gomes: Não fez!
Renata Luiza: Quando um professor entra na sala de
aula e diz que iniciará o estudo dos números complexos, os alunos pensam que
são números, no mínimo, muito complicados. Ao saber que também existem números
chamados de imaginários os alunos dirão que tais números, por serem
imaginários, não existem, e, portanto, para que estudá-los?
Bem, a questão central desta página
é "Como surgiram os Números
Complexos?”.
O primeiro matemático de que se tem
conhecimento de se ter deparado com um problema que envolvia números complexos
foi Héron de Alexandria (séc. I dC)
no livro Stereometrica. Este pretendia resolver
Ö(81-144) = Ö(-63)
mas como não
havia o domínio atual sobre estes números, abandonou o seu cálculo.
Por volta do ano 275 dC, Diophanto (200-284 aprox.) ao resolver
um problema deparou-se com a equação
24x2 - 172x + 336 = 0
como
concluiu que não tinha soluções reais, não viu necessidade de dar sentido à
raiz Ö-167.
Na Índia, por volta do ano 850, Mahavira (800-870 aprox.) escrevia:
"(...) como na natureza das coisas um negativo não é um quadrado, ele não tem,
portanto, raia quadrada." Ou seja, negou à partida, a existência de
números negativos cuja raiz quadrada devolve um outro número.
Bhaskara (1114-1185 aprox.), um dos indianos
que mais perto chegou das ideias da álgebra moderna (conhecia a regra
"menos por menos dá mais", trabalhava com coeficientes negativos, etc.)
reconhecia que a equação x2 - 45x = 250 era satisfeita por dois valores x = 5 e
x = -5, mas, dizia que não considerava a segunda pois as pessoas não
"apreciavam" raízes negativas.
Gerônimo
Cardano (1501-1576)
considerava que o aparecimento de raízes quadradas de números negativos na
resolução de um problema indicava que o mesmo não tinha solução. No entanto,
foi Cardano que, em 1545, mencionou pela primeira vez os números complexos. Na
sua obra Ars Magna de Cardano, falava do seguinte problema: "Determinar
dois números cuja soma seja 10 e o produto seja 40". Para tal, considerou
as expressões 5 + Ö15 e 5 - Ö-15. Cardano ficou por aqui, não dando significado
a estas expressões, pondo de lado a "tortura mental" envolvida, mas,
teve o mérito de ter sido o primeiro a considerá-las, até porque neste tempo os
números negativos eram evitados.
A partir disto é possível derrubar a
ideia errada de que os números complexos surgiram com as equações do segundo
grau. Os números complexos apareceram sim, a partir das equações de terceiro
grau.
Mas, foram preciso cerca de 25 anos
para este tema ser de novo considerado, por Raffaelle Bombelli (1526-1572) numa obra de nome Algebra.
Ao resolver a equação x3 = 15x + 4, Bombelli utilizou a
"fórmula de Cardano" obtendo a seguinte solução (em notação moderna):
x = 3Ö(2 + Ö-121) + 3Ö(2 - Ö-121)
Ele achou estranho este resultado
porque conhecia todas as raízes da equação, entre as quais x = 4. Teve então a
estranha ideia de procurar a e b positivos tais que:
a + bÖ-1 = 3Ö(2 + Ö-121)
a - bÖ-1 = 3Ö(2 - Ö-121)
Com alguma manipulação algébrica,
usando as mesmas regras que usava para os números reais, mais a propriedade (Ö-1)2
= -1, chegou ao resultado a = 2 e b = 1, donde sai x = 4. O próprio Bombelli
não estava bem seguro do que havia criado. Para os demais matemáticos da época,
os números complexos eram vistos com suspeita e quantos muito tolerados, na
falta de melhor coisa. É de referir que alguns matemáticos da época procuraram
maneiras de evitar o uso de tais números. Entre eles, Cardano foi o que mais
tentou evitar as "torturas mentais" envolvidas no uso de raízes
quadradas de negativos. No seu livro De Regula Aliza, de 1570, procurou
artifícios que contornassem o uso de tais raízes na resolução de equações de 3º
grau obtendo, somente, resultados vagos.
Raffaelle
Bombelli apresentou
na sua obra Algebra as leis algébricas que regiam os cálculos entre números da
forma a + bÖ -1. Em particular, mostrou que as quatro operações aritméticas
sobre números complexos produzem números desta forma. Ou seja, o conjunto dos
complexos é fechado para estas operações.
Em 1629, Albert Girard (1595-1632) utiliza, efetivamente, o símbolo Ö-1
quando enuncia as relações entre raízes e coeficientes de uma equação.
Um grande passo no estudo dos
números complexos foi a sua representação visual. Em 1797, o dinamarquês Caspar Wessel (1745-1818) representou,
pela primeira vez, geometricamente os números complexos, estabelecendo uma
correspondência objetiva entre estes e os pontos do plano. Este trabalho foi
levado ao esquecimento, talvez por ter sido publicado em dinamarquês e só por
volta de 1806, quando publicado em francês por Jean Argand (1768-1822) ganhou o devido respeito. Por este motivo, esta
representação ficou, indevidamente, ligada ao nome de Argand. O símbolo i, para
a representação de Ö-1, foi criado por Leonard Euler, mas, só após o seu uso
por Gauss (1777-1855) em 1801, é que
foi aceite. A expressão número complexo
foi introduzida em 1832, por Gauss.
É possível dizer que, apesar da sua história
ser recente, os números complexos envolveu o trabalho de vários matemáticos
continuando, ainda hoje, muitas questões em aberto.
Thaina Fernanda: Unidade imaginária: define-se a unidade imaginária , representada pela
letra i , como sendo a raiz quadrada
de -1. Pode-se escrever então: i = Ö-1 .
Observe que a partir dessa definição , passam a ter sentido certas
operações com números reais , a exemplo das raízes quadradas de números
negativos .
Ex: Ö-16 = Ö16 . Ö-1 = 4.i = 4i
Potências de i :
i0 = 1
i1 = i
i2 = -1
i3 = i2 . i = -i
i4 = (i2)2 = (-1)2 = 1
i5 = i4 . i = 1.i = i
i6 = i5 . i = i . i = i2 = -1
i7 = i6 . i = -i , etc.
Percebe-se que os valores das potências de i se repetem no ciclo
1 , i , -1 , -i , de quatro em quatro a partir do expoente zero.
Portanto, para se calcular qualquer potência inteira de i , basta
eleva-lo ao resto da divisão do expoente por 4. Assim , podemos resumir:
i4n = ir onde r = 0 , 1 , 2 ou 3. (r é o resto da divisão de n por 4).
Exemplo: Calcule i2001
Ora, dividindo 2001 por 4, obtemos resto igual a 1. Logo i2001 = i1 = i
.
NÚMERO COMPLEXO
Definição: Dados dois números reais a e b , define-se o número complexo
z como sendo:
z = a + bi , onde i = Ö-1 é a unidade imaginária .
Exs: z = 2 + 3i ( a = 2 e b = 3)
w = -3 -5i (a = -3 e b = -5)
u = 100i ( a = 0 e b = 100)
NOTAS:
a) diz-se que z = a + bi é a forma binômia ou algébrica do complexo z .
b) dado o número complexo z = a + bi , a é denominada parte real e b
parte imaginária.
Escreve-se : a = Re(z) ; b = Im(z) .
c) se em z = a + bi tivermos a = 0 e b diferente de zero, dizemos que z
é um imaginário puro . Ex: z = 3i .
d)se em z = a + bi tivermos b = 0 , dizemos que z é um número real .
Ex: z = 5 = 5 + 0i .
e)do item (c) acima concluímos que todo número real é complexo, ou seja,
o conjunto dos números reais é um subconjunto do conjunto dos números
complexos.
f)
um número complexo z = a + bi pode também ser representado como um par ordenado
z = (a,b)
Thamy Rafaella: Cardano 1545 ao tentar resolver a cúbica x 3 = 4 + 15x , a qual ele sabia ter raiz verdadeira x = 4, constatou que a regra de dal Ferro-Tartaglia produzia a seguinte expressão ( em notação moderna ) :
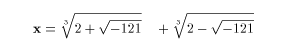 |
Deparando-se com o termo 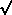 - 121 , ele não conseguiu ver como "destravar" o calculo, de modo a fazer a regra chegar ao esperado x = 4.
- 121 , ele não conseguiu ver como "destravar" o calculo, de modo a fazer a regra chegar ao esperado x = 4.
Foram precisos mais de 25 anos para Bombelli, em 1572, atinar como resolver o impasse . Esse disse ter tido a "idéia louca" de operar com as quantidades da forma a + b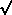 -1 sob as mesmas regras que se usa com os números reais, mais a propriedade
-1 sob as mesmas regras que se usa com os números reais, mais a propriedade
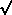 - 121 , ele não conseguiu ver como "destravar" o calculo, de modo a fazer a regra chegar ao esperado x = 4.
- 121 , ele não conseguiu ver como "destravar" o calculo, de modo a fazer a regra chegar ao esperado x = 4.Foram precisos mais de 25 anos para Bombelli, em 1572, atinar como resolver o impasse . Esse disse ter tido a "idéia louca" de operar com as quantidades da forma a + b
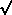 -1 sob as mesmas regras que se usa com os números reais, mais a propriedade
-1 sob as mesmas regras que se usa com os números reais, mais a propriedade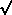 -1 )2 = -1
-1 )2 = -1
para assim conseguir "destravar" a regra, fazendo-a produzir o desejado x = 4.

Nenhum comentário:
Postar um comentário