NÚMEROS COMPLEXOS
Além de historicamente errada, essa extremamente comum "explicação" para o surgimento dos números complexos é um absurdo. Com efeito, por que alguém iria buscar raízes num campo numérico desconhecido?
Até cerca de 1 650 dC, em respeito à orientação geométrica da matemática grega, as únicas raízes consideradas como legítimas ou verdadeiras eram as que correspondiam à grandezas geométricas ou físicas : podiam ser interpretadas como comprimentos, áreas, volumes, massas, etc. Diríamos hoje: correspondiam a números reais POSITIVOS .
Por exemplo, Bhaskara, que foi um dos indianos que mais perto chegou da idéia da moderna álgebra ( conhecia a regra menos vezes menos dá mais, trabalhava com equações de coeficientes negativos, etc ), reconhecia que a equação
era satisfeita por dois valores, x = 5 e x = - 5, mas dizia que não considera-se a segunda pois as pessoas não apreciam raízes negativas .
Resumindo, até o surgimento dos cartesianos, c. 1650, as raízes eram divididas em verdadeiras ( correspondiam aos reais positivos) e falsas ( que correspondiam aos reais negativos e não eram consideradas como legítimas ). As únicas e raras ocorrências de raízes negativas nesse período surgiam em problemas de contabilidade, onde eram interpretadas como dívidas.
Resumindo, até o surgimento dos cartesianos, c. 1650, as raízes eram divididas em verdadeiras ( correspondiam aos reais positivos) e falsas ( que correspondiam aos reais negativos e não eram consideradas como legítimas ). As únicas e raras ocorrências de raízes negativas nesse período surgiam em problemas de contabilidade, onde eram interpretadas como dívidas.
Cardano 1545 ao tentar resolver a cúbica x 3 = 4 + 15x , a qual ele sabia ter raiz verdadeira x = 4, constatou que a regra de dal Ferro-Tartaglia produzia a seguinte expressão ( em notação moderna ) :
 |
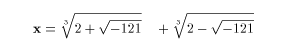Deparando-se com o termo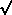 
- 121 , ele não conseguiu ver como "destravar" o calculo, de modo a fazer a regra chegar ao esperado x = 4.
Foram precisos mais de 25 anos para Bombelli, em 1572, atinar como resolver o impasse . Esse disse ter tido a "idéia louca" de operar com as quantidades da forma a + b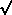 -1 sob as mesmas regras que se usa com os números reais, mais a propriedade
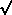- 121 , ele não conseguiu ver como "destravar" o calculo, de modo a fazer a regra chegar ao esperado x = 4.Foram precisos mais de 25 anos para Bombelli, em 1572, atinar como resolver o impasse . Esse disse ter tido a "idéia louca" de operar com as quantidades da forma a + b
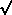-1 sob as mesmas regras que se usa com os números reais, mais a propriedade 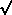-1 )2 = -1
para assim conseguir "destravar" a regra, fazendo-a produzir o desejado x = 4.
O próprio Bombelli não estava bem seguro do que havia criado, chegando mesmo a dizer que eram uma nova espécie de raízes quadradas ... que tem regras diversas das outras. Para os demais matemáticos da época, os números complexos eram vistos com suspeita e quanto muito tolerados, na falta de melhor coisa. Até o nome que receberam, números SOFÍSTICOS, espelhava bem a situação.
É de se acrescentar que alguns matemáticos da época procuraram descobrir maneiras de se evitar o uso dos complexos. Entre eles, o que mais procurou evitar as torturas mentais envolvidas com o uso de raízes quadradas de negativos foi Cardano. Em seu difícil livro De Regula Aliza, de 1 570, Cardano procurou inventar artifícios de cálculo que evitassem o uso de raízes quadradas de negativos quando da aplicação das regras de resolução de cúbicas. Conseguiu apenas magros resultados. Foram necessários trezentos anos para que, em 1 890, Capelli conseguisse provar que isso é em geral impossível de conseguir.
O próprio Bombelli não estava bem seguro do que havia criado, chegando mesmo a dizer que eram uma nova espécie de raízes quadradas ... que tem regras diversas das outras. Para os demais matemáticos da época, os números complexos eram vistos com suspeita e quanto muito tolerados, na falta de melhor coisa. Até o nome que receberam, números SOFÍSTICOS, espelhava bem a situação.
É de se acrescentar que alguns matemáticos da época procuraram descobrir maneiras de se evitar o uso dos complexos. Entre eles, o que mais procurou evitar as torturas mentais envolvidas com o uso de raízes quadradas de negativos foi Cardano. Em seu difícil livro De Regula Aliza, de 1 570, Cardano procurou inventar artifícios de cálculo que evitassem o uso de raízes quadradas de negativos quando da aplicação das regras de resolução de cúbicas. Conseguiu apenas magros resultados. Foram necessários trezentos anos para que, em 1 890, Capelli conseguisse provar que isso é em geral impossível de conseguir.
Nenhum comentário:
Postar um comentário